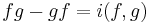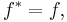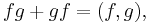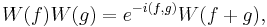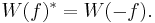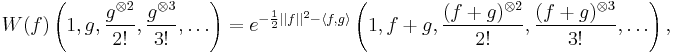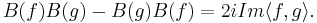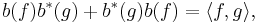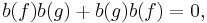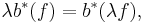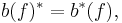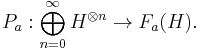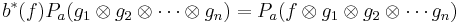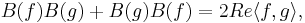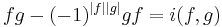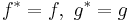CCR and CAR algebras
In Mathematics and Physics the CCR and CAR algebras arise from the study of canonical commutation relations in Bosonic and Fermionic quantum mechanics. They are used in mathematical formulations of quantum statistical mechanics and quantum field theory.[1]
Contents |
CCR and CAR as *-algebras
Let  be a real vector space equipped with a nonsingular real antisymmetric bilinear form
be a real vector space equipped with a nonsingular real antisymmetric bilinear form 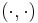 (i.e. a symplectic vector space). The unital *-algebra generated by elements of
(i.e. a symplectic vector space). The unital *-algebra generated by elements of  subject to the relations
subject to the relations
for any 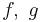 in
in  is called the canonical commutation relations (CCR) algebra. The uniqueness of the representations of this algebra when
is called the canonical commutation relations (CCR) algebra. The uniqueness of the representations of this algebra when  is finite dimensional is discussed in the Stone-von Neumann theorem.
is finite dimensional is discussed in the Stone-von Neumann theorem.
If  is equipped with a nonsingular real symmetric bilinear form
is equipped with a nonsingular real symmetric bilinear form 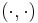 instead, the unital *-algebra generated by the elements of
instead, the unital *-algebra generated by the elements of  subject to the relations
subject to the relations
for any 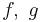 in
in  is called the canonical anticommutation relations (CAR) algebra.
is called the canonical anticommutation relations (CAR) algebra.
The C*-algebra of CCR
Let  be a real symplectic vector space with nonsingular symplectic form
be a real symplectic vector space with nonsingular symplectic form 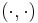 . In the theory of operator algebras the CCR algebra over
. In the theory of operator algebras the CCR algebra over  is the unital C*-algebra generated by elements
is the unital C*-algebra generated by elements 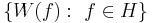 subject to
subject to
These are called the Weyl form of the canonical commutation relations and, in particular, they imply that each 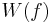 is unitary and
is unitary and 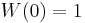 . It is well known that the CCR algebra is a simple non-separable algebra and is unique up to isomorphism.[2]
. It is well known that the CCR algebra is a simple non-separable algebra and is unique up to isomorphism.[2]
When  is a Hilbert space and
is a Hilbert space and 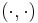 is given by the imaginary part of the inner-product, the CCR algebra is faithfully represented on the symmetric Fock space over
is given by the imaginary part of the inner-product, the CCR algebra is faithfully represented on the symmetric Fock space over  by setting
by setting
for any 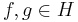 . The field operators
. The field operators 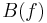 are defined for each
are defined for each 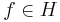 as the generator of the one-parameter unitary group
as the generator of the one-parameter unitary group 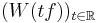 on the symmetric Fock space. These are self-adjoint unbounded operators, however they formally satisfy
on the symmetric Fock space. These are self-adjoint unbounded operators, however they formally satisfy
As the assignment 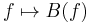 is real-linear, so the operators
is real-linear, so the operators 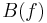 define a CCR algebra over
define a CCR algebra over 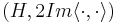 in the sense of Section 1.
in the sense of Section 1.
The C*-algebra of CAR
Let  be a Hilbert space. In the theory of operator algebras the CAR algebra is the unique C*-completion of the complex unital *-algebra generated by elements
be a Hilbert space. In the theory of operator algebras the CAR algebra is the unique C*-completion of the complex unital *-algebra generated by elements 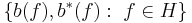 subject to the relations
subject to the relations
for any 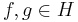 ,
, 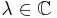 . When
. When  is separable the CAR algebra is an AF algebra and in the special case
is separable the CAR algebra is an AF algebra and in the special case  is infinite dimensional it is often written as
is infinite dimensional it is often written as 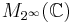 .[3]
.[3]
Let 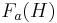 be the antisymmetric Fock space over
be the antisymmetric Fock space over  and let
and let 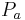 be the orothogonal projection onto antisymmetric vectors:
be the orothogonal projection onto antisymmetric vectors:
The CAR algebra is faithfully represented on 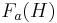 by setting
by setting
for all 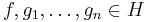 and
and 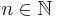 . The fact that these form a C*-algebra is due to the fact that creation and annihilation operators on antisymmetric Fock space are bona-fide bounded operators. Moreover the field operators
. The fact that these form a C*-algebra is due to the fact that creation and annihilation operators on antisymmetric Fock space are bona-fide bounded operators. Moreover the field operators 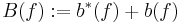 satisfy
satisfy
giving the relationship with Section 1
Superalgebra generalization
Let  be a real
be a real 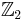 -graded vector space equipped with a nonsingular antisymmetric bilinear superform
-graded vector space equipped with a nonsingular antisymmetric bilinear superform 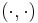 (i.e.
(i.e. 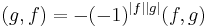 ) such that
) such that 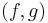 is real if either
is real if either  or
or  is an even element and imaginary if both of them are odd. The unital *-algebra generated by the elements of
is an even element and imaginary if both of them are odd. The unital *-algebra generated by the elements of  subject to the relations
subject to the relations
for any two pure elements 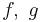 in
in  is the obvious superalgebra generalization which unifies CCRs with CARs: if all pure elements are even, one obtains a CCR, while if all pure elements are odd, one obtains a CAR.
is the obvious superalgebra generalization which unifies CCRs with CARs: if all pure elements are even, one obtains a CCR, while if all pure elements are odd, one obtains a CAR.
The graded generalizations of Weyl and Clifford algebras allow the basis-free formulation of the canonical commutation and anticommutation relations in terms of a symplectic and a symmetric non-degenerate bilinear form. In addition the binary elements in this graded Weyl-algebra give a basis-free version of the commutation relations of the symplectic and pseudo-orthognal Lie algebras.[4]
See also
- canonical commutation relation
- Stone-von Neumann theorem
- Bose-Einstein statistics
- Fermi-Dirac statistics
- Heisenberg group
- Weyl algebra
- Bogoliubov transformation
- (−1)F
References
- ^ Bratteli, Ola; Robinson, Derek W. (1997). Operator Algebras and Quantum Statistical Mechanics: v.2. Springer, 2nd ed. ISBN 978-3540614432.
- ^ Petz, Denes (1990). An Invitation to the Algebra of Canonical Commutation Relations. Leuven University Press. ISBN 978-9061863601. http://www.math.bme.hu/~petz/ccr.html.
- ^ Evans, David E.; Kawahigashi, Yasuyuki (1998). Quantum Symmetries in Operator Algebras. Oxford University Press. ISBN 978-0198511755..
- ^ Roger Howe (1989). "Remarks on Classical Invariant Theory". Transactions of the American Mathematical Society 313: 539–570. doi:10.1090/S0002-9947-1989-0986027-X. JSTOR 2001418.